
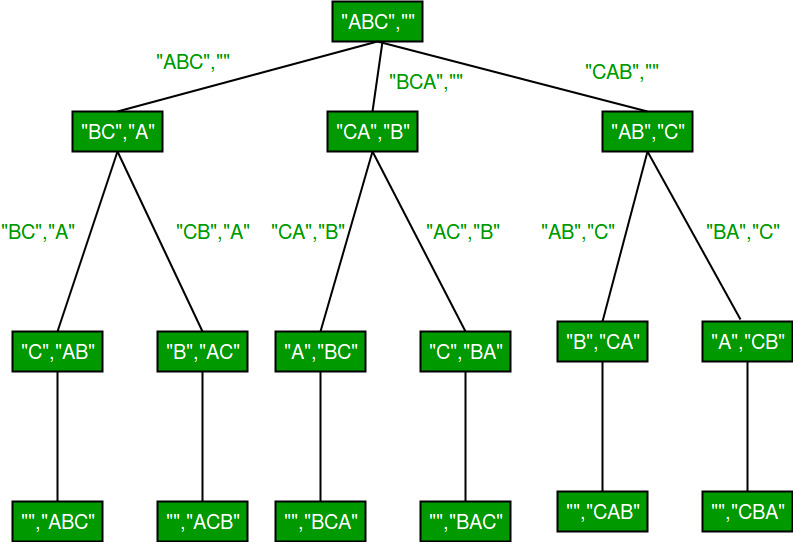
The approach would be to take out the first char and keep it constant and permute the rest of the characters and use recursion to permute the rest of the string except the first character. Following is the java program to find permutation of a given string. A string of length n can have a permutations of n!. For example, the permutation of ab will be ab and ba. Permutation is the each of several possible ways in which a set or number of things can be ordered or arranged.
#Permute a string code
The GitHub repo containing the solution code also comes with a test suite, so you can practice or play around with finding alternate solutions for this problem if you like.Write a java program to find all the permutations of any given string. While not specifically applicable to every algorithm problem, and not always the most performant or elegant solution, it’s a reliable workhorse model that can serve you well! I have found this model to be a really handy tool that reliably provides me with a place to start when tackling algorithmic challenges. So what was our master theorem based approach again?ġ: Establish a base case - if our input’s size is less than a certain constant, solve it directly without recursion.Ģ: If the input is bigger than said constant, break it down into smaller pieces.ģ: Call the function recursively on the pieces, until they are small enough to be solved directly.Ĥ: Combine the results from the pieces, and return the completed solution. Perfect! 🌟 A master theorem based approach allowed us to quickly break this problem down into bite sized pieces and begin returning correct results, leaving only a few tweaks needed here and there to deliver our solution in exactly the desired format. Let’s run findPermutation with this addition. If this is true, we can continue, which will essentially skip the current iterative loop and move on to the next. indexOf returns the first index of a character, so if we’ve already run findPermutations for an “a”, for example, the indexOf(“a”) will be different than the index of char, the current, later “a”.

There are a lot of different ways to remove superfluous elements, but I chose to use Javascript’s indexOf method to identify if the current character has already been run through our findPermutations method. If (!string || typeof string != "string") If my final solution may return more than one “correct” element (in this case, permutations), I’ll need a place to store them before I return the complete solution.Ģ: Iterate! If I need to find all the ordered combinations of characters in a string, creating a loop to iterate through all the characters in a string seems like a decent place to start.
When I see a challenge like this, my first instinct is two do two things:ġ: Make an empty array. So we’ve figured out what a permutation is, and established that (depending on the length of the string) we may be looking for a lot of them. Suddenly, this whole string-manipulation problem seems a bit more intimidating. As a part of trying to get better with backtracking I wrote the following code to permute a string: def permute (str): permuteHelper (str,'') def permuteHelper (str,chosen): if not str: print (chosen) else: for i in range (len (str)): choose currChar str i The char we choose chosen + currChar Add chosen char to chosen.

The whole point of combination locks is that a relatively small amount of numbers can create a large enough number of ordered combinations to prohibit casual opening. However, it does not need to be an existing word, but can simply be a re-arrangement of the characters.Īn example of permutations of something other than a string would be this:įor just three colors, we can have six different permutations, or ordered combinations of those colors.Īnother example of permutations would be a combination lock: A string permutation is similar to an anagram. So every string has a number of permutations into which its characters could be re-arranged. The solution model I explore here utilizes tools and concepts that I find broadly valuable for the solution of algorithmic challenges, and methods that I find intuitive for string manipulation within Javascript.įirst things first: What is a permutation?Ī way, especially one of several possible variations, in which a set or number of things can be ordered or arranged. Note : There is more than one way to solve this problem. Why? While the task of manipulating a string may seem familiar on its surface, actually finding a complete solution requires us to handle some unexpected complexity, which provides the opportunity to utilize a recursive tree and build a bit of familiarity with the master theorem. When I sat down to solve this problem, I found it to be a great algorithm challenge. Given a string, return all permutations of the string. GitHub repo with completed solution code and test suite.


 0 kommentar(er)
0 kommentar(er)
